What’s in a Gabor patch?

In one of the first classes of my first neuroimaging course, a confusing dialogue took place.

Professor: In this experiment, people looked at a cross at the center of the screen while a Gabor patch was presented either to the left or to the right of the cross…

Student: Excuse me, what’s a Gabor patch?

Professor: Oh. Oh! Why that’s a sinusoid convolved with a Gaussian!

He was smiling at us while ignoring the the Gabor patch that was prominently displayed on the screen just behind him. His eyebrows went up expectantly. His whole pose said: “Yes? It’s clear now?”

Student: Er…

Professor: No? Here, I’ll show you!

Still ignoring the presentation screen, he turned towards the blackboard. On it, he drew a sinusoid. And beneath the sinusoid – a Gaussian.

“And then, you convolve them!!”

The student gave up. He maybe had some vague idea about convolution, but no good intuition of it. What he really needed was a finger pointed towards the right place on the screen: this is a Gabor patch.

This could be a story about how I sometimes feel like that student. Or a story about teaching. Or perhaps about how perfectly accurate information can sometimes still appear nonsensical. But what I’d really like to focus on, is that a Gabor patch is more than just a sinusoid convolved with a Gaussian.

Say you had a batch of kittens that happened to be raised in an environment deprived of all but one orientation – vertical. All the kittens would ever see were vertical stripes. What would happen if, a few months later, these kittens got to interact with the world as it is?

A kitten raised in a vertically-striped environment.

Blakemore, C & Cooper GF (1970). Development of the brain depends on the visual environment.

Nature (228), 477-478

 

What happens is that, after a bit of a shaky start, they learn to make sense of the visual world. They start exploring, playing, acting like kittens. But if their eyes are turned towards a thin, elongated, horizontally oriented object, for instance a black cable stretched across a white carpet, they’ll act as if it doesn’t exist. They won’t startle if it suddenly moves towards them, or pounce on it if it jiggles. They’ll be selectively blind to it, even though their eyes work just fine. The root of their problem is in the brain.

The primary visual cortex – the first in a series of cortical areas that process visual information – is sensitive to line orientation. Certain cells there, called simple cells (or bar detectors, or edge detectors) become active to different degrees depending on the orientation of the edges of observed objects. If we were to walk along the surface of the primary visual cortex, we’d slowly be moving from vertical orientation areas to areas tuned to more and more tilt. This means that one group of cells will become very active when a vertical bar is presented, another group of cells if we tilt the bar a bit, and yet another group of cells if the bar is horizontal. The cells ‘tuned’ to vertical orientations will still fire away to bars of nonvertical orientations, just less and less as the difference between the ‘preferred’ vertical orientation and displayed other orientation increases.

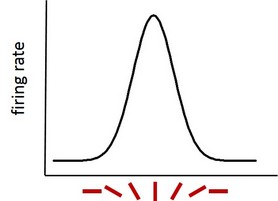
Responsivity of a neuron tuned to vertical bars as a function of actual bar orientation.

In the case of the kittens, the cells that should have been responsive to horizontal orientations, began to respond to other orientations due to sensory deprivation throughout this critical period of development. That left no cells to respond to horizontal stimuli, and so the visual signal extinguished at this stage of neural processing.

Once we found out about orientation tuning, we could make sense of a certain perceptual phenomenon. Namely, if we continuously look at the same oriented bar, then, our ability to judge the tilt of subsequent, similarly oriented bars will briefly decrease, but this effect will systematically weaken for bars tilted further away. We now know that this is due to neural fatigue – the more a neuron was firing before, the more fatigued it will be later on, and thus less able to encode the orientation properly. 

And how do we know all this? Thanks to thousands of experiments with Gabor patches. Gabor patches are stimuli that drive early visual activity in a controlled fashion. They look like a series of black and white bars, they can be oriented every which way, they can be made easily discernible or difficult to see, small or large, central or peripheral, rotating or stationary. They are a solid presence in any vision lab. 

What I witnessed that day in class was a misunderstanding, an honest mistake. My professor did not mean to bypass the brain and the mind, or to suggest that perception ends with a physical description of stimulation. He simply assumed the student knew about orientation tuning, and he attempted to give extra information.

But there is even more to a Gabor patch than how it drives the primary visual cortex. Properties of early visual processing are enormously influential on how we think about the brain as a whole. They inspire the belief that somewhere in there, there will be a neural code for perceiving time, or space, or our position in that space, or the meaning of words, the beauty of certain melodies, or for complex emotions such as the pain of social rejection, our ability to judge what someone else might be thinking, and even further, our sense of self, political attitudes, or character traits. These neural patterns might not be as easily discernible to us as observers, but we believe the code is there, ready to be pulled out and analyzed, matched one to one with cognitive concepts, and that cognition can in principle be perfectly linked back to the rules guiding neural firing. Taken even further, once we crack this code, it should be possible to build machines with identical information processing capacities to ours, indistinguishable from ourselves except in looks. 

Nobody thinks this is an easy task. Even with the simple cells, the reality is far more complex than assigning a neuron to an orientation on one side, and linking it to a percept on the other side. To begin with, the percept is connected not to single neurons, but to the relative amounts of activity in neurons that favour different orientations. The relationship between the percept and this activity distribution is not straightforward either. If we were to observe a vertical bar, but tilt our head or entire body sideways, so that the bar would now be slanted relative to our eyes, neurons that prefer slanted orientations should fire away. In reality, it still continues to be a vertical bar according to the neurons in our primary visual cortex (and we also perceive it as vertical). This is because vestibular information is integrated with orientation information, and corrected for. Furthermore, orientation and space are co-coded: the pattern of incrementally tilted orientations that tile the surface of the primary visual cortex, repeats many times over. This allows for tilt to be adequately perceived in different parts of the visual field. Simple cells capture other information as well, such as how busy a visual display is – a Gabor patch with many thin stripes will have a different impact on simple cells than a Gabor patch with a few thick stripes. Some simple cells will have broad tuning curves; others will have narrow ones. Some will integrate input from the previous level of processing, the thalamus, in a mostly a additive manner, others will involve more complex computations. On top of all this, simple cells selectively inhibit each other, and on top of that, their activity flexibly adapts based on input from higher-order areas. Imagine if they weren’t simple!

Regardless of this complexity, the links between line orientation and neural activity, and between neural activity and perception, are fairly straightforward. Enough so, in fact, that perceptual oddness can lead to educated guesses about what goes on in the brain, like in case of the café wall illusion, where the surrounding visual context influences our perception of orientation, possibly due to local inhibition. 

The café wall illusion.

The bricks appear trapezoidal and the mortar slanted.

The bricks are however all rectangular and of the same size,

and the mortar between them is parallel to the ground.

 

Should we expect such clear-cut links between cognitive processes and neural activity to be the norm? It is not unusual to see orientation tuning described as an introduction to much grander ideas of what the brain is for – as a prototypical example of how we work. It is also very common for research papers to open up with a general cognitive question (How do we identify our car out of hundreds in the parking lot? How do we navigate walking down a busy street? Why are we surprised when a prolonged source of noise suddenly goes silent?), but to close with a fine-grained neural level of description of an experimental effect. To the uninitiated, this might make it seem that the links to the cognitive phenomenon are considered so self-explanatory that they don’t need further fleshing out. In reality, it is more likely to reflect the belief that the space between neural activity and cognitive processing can in principle be filled, and that slowly, and with much effort, we will fill it completely – following the good example of orientation tuning.

However, as the phenomena we study grow in complexity, it quickly gets incredibly hard to translate insights from neural to cognitive. Much of orientation perception is beautifully contained in the activity of simple cells in the primary visual cortex, but it would be woefully inadequate to define learning exclusively through synaptic plasticity. Even when all the relevant neural activity is precisely captured, we still need a principled way to connect it to cognition, and this principled way almost never emerges from looking harder at neural tissue. 

If we were to ask whether mental phenomena have to rely on neural activity, the answer is clearly yes. In this sense, all of cognition is reducible down to simple, tangible, uncontroversial building blocks, which are combined based on a finite number of clear guiding principles. From this simplicity, unanticipated complexity emerges. In this sense, learning can in principle be described on the neural level, and we can in principle build machines that are cognizant in the same way we are. Simple cell activity that arises when we observe a Gabor patch is a good example of how this might work, for a mental function of any complexity.

From a completely different perspective, some important phenomena reside both within people and between them. Our sense of identity, for instance, is a mix of personal features and how these features compare to other people’s. One salient property of mine is that I am a foreigner. This is reflected in how I process certain information relative to locals. For example, I cannot discern certain sounds spoken in the local accent, because I haven’t grown up with them, and their signal will extinguish in my auditory cortex just like the horizontal orientation extinguished in those unfortunate kittens. My being a foreigner can be discussed in terms of differences in neural activity, perhaps with great precision, but is that a sensible thing to do? My differences with locals will change as I move from country to country, and within any country, other foreigners might differ from locals in ways unrelated to mine. It makes more sense to discuss any such neural differences as a function of cultural differences, rather than a function of the foreign brain giving rise to the foreign mind. I do not have a foreign brain: a have a brain, and I am a foreigner. Taken to its extreme, any act of symbolization can be viewed as culturally co-constructed in the same vein as foreignness, and is therefore, in some crucial and often neglected sense, not a feature of the brain. And conscious thought requires symbolization.

People who are interested in the goings-on at these two extremes – reduction of cognitive phenomena to neural activity on the one hand, and refraction of these phenomena through the cultural and interpersonal lens on the other, tend to see the other position as true but trivial, devoid of real explanatory power. I have a hunch that this might be due to a disagreement about the nature of causality, and whether it can flow in one direction or many. In any case,  the relationship between the neural and the cognitive side of the coin is a nuanced one.

Following these nuances, we might want to ask whether within a person any mental phenomenon can necessarily be fully related to a precise, unvarying neural state, and if, by extension, we could in principle always use a neural state to describe a cognitive outcome. The answer to this question is no. Many neural states can lead to the same cognitive outcome (like when you solve the same math problem by leaning on your number sense, or on visualization, or on the ability to verbalize), and different cognitive outcomes might stem from a single state (like when your excitement turns into anxiety or euphoria).  

But maybe there is some essential neural activity hidden in this variability, or maybe this essence is shifted into one pattern or another depending on what the rest of the brain is doing? If we could completely describe this background neural activity, could we then know how the mental activity would coalesce? Perhaps. More likely, however, is that the emergent properties of cognition follow rules of their own, rules that do not exist a level down. For example, it can make sense to say that one thought caused another, while at the same time it might not make sense to say that the neural pattern underlying the first thought, caused the neural pattern underlying the second thought. Without referring to cognition, the link between the two neural patterns is in no way obvious. This means that the way the mind is organized might not be the best guiding principle to unearthing how the brain is organized – that the mind has a mind of its own.

Conversely, our assumptions that neural effects easily capture cognitive phenomena are not a given, and the assumptions about this neuro-cognitive connection should not be glossed over. Personally, whenever I reach the the end of a cognitive neuroscience paper, I try to ask myself whether I can now say something new about the cognitive phenomenon that was claimed to be studied – but without referring to the brain. If I cannot, then perhaps cognition was not the main hero of the story after all, but rather a character with a supporting role. This principle helps me remember that neural activity is cognition in the same way that a Gabor patch is a sinusoid convolved with a Gaussian: neural activity explains cognition in unquestioningly true terms, that are at the same time unquestioningly limited.